Beyond Distributed Compilation: A New Paradigm for Heterogeneous Computing
Disclaimer: This article was generated by artificial intelligence.
Beyond Distributed Compilation: A New Paradigm for Heterogeneous Computing
 Figure 1: The complexity of modern distributed systems
Figure 1: The complexity of modern distributed systems
The Challenge
Consider the case of Large Language Models (LLMs). Today, we have specialized systems like vLLM or Text Generation Inference (TGI) that are meticulously optimized for NVIDIA GPUs. These optimizations are carefully tuned for the current GPU architecture, where memory bandwidth is often the limiting factor. But what happens when a new GPU architecture emerges with vastly different characteristics - perhaps one with much higher memory bandwidth and lower latency? Suddenly, all that carefully crafted code needs to be rewritten.
The problem extends beyond just GPUs. What if you want to run the same LLM on CPUs, which have entirely different performance characteristics? Or across multiple nodes, where network latency and bandwidth become critical factors? With a high-bandwidth, low-latency InfiniBand connection, you might want one data layout, but with a slower network, you’d need a completely different approach.
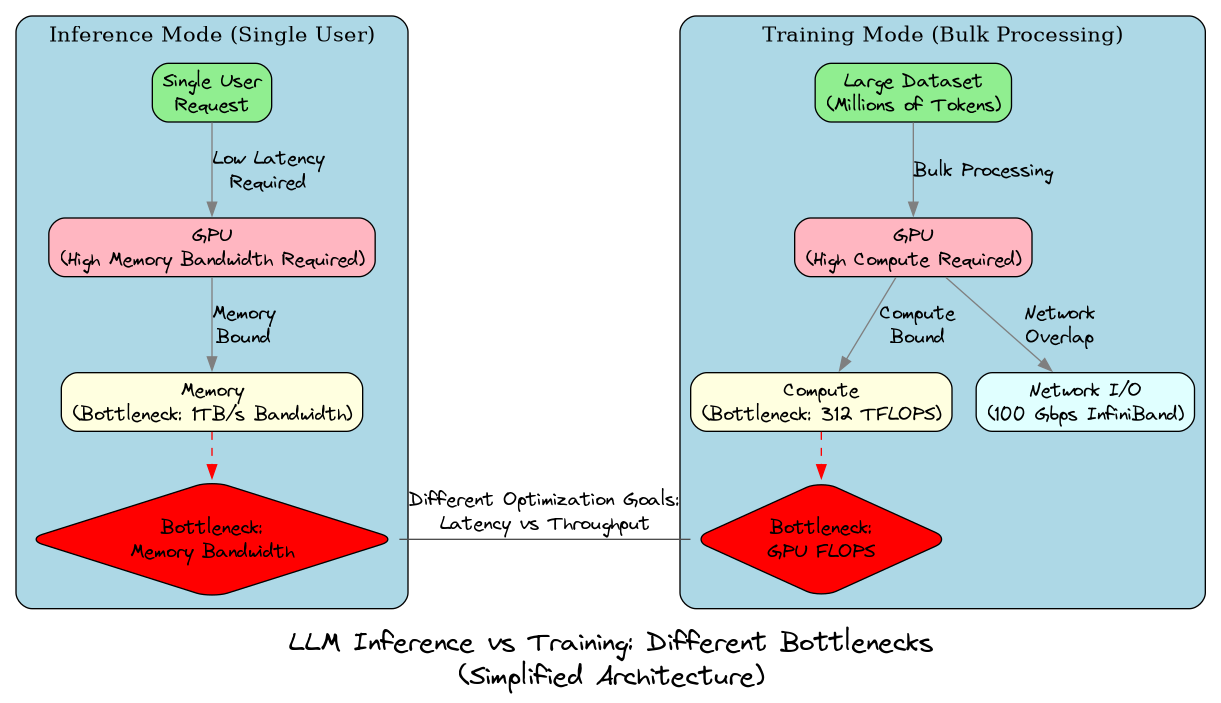 Figure 2: Different hardware architectures require different optimization strategies
Figure 2: Different hardware architectures require different optimization strategies
This situation is strikingly similar to the early days of computing, when each CPU architecture required its own specialized assembly code. Then came C, and with it, a revolutionary idea: write your code once in a system-agnostic way, and let the compiler handle the translation to the specific instruction set. The compiler could optimize for the target architecture, taking into account its unique characteristics.
We need a similar revolution for distributed systems. Instead of writing specialized code for each hardware configuration, we need a language that describes the problem at a high level, independent of the underlying hardware. The compiler would then handle the complex task of optimizing for the specific architecture, taking into account:
- Memory bandwidth and latency
- Network topology and characteristics
- Cache hierarchies
- Hardware-specific schedulers
- Data movement patterns
When new hardware emerges, we wouldn’t need to rewrite our code - we’d just need to recompile it. The compiler would understand the new architecture’s characteristics and generate optimized code accordingly. This would free developers to focus on solving problems rather than wrestling with hardware-specific optimizations.
The Problem
The fundamental challenge stems from a theoretical limitation: Turing-complete programming languages face the halting problem. This means it’s impossible for a compiler to determine if a program will halt, let alone predict how long it will run. This uncertainty makes it extremely difficult for compilers to reason about program optimization. As a result, developers must manually profile their code, identify hot loops, optimize cache usage, and adjust data structures to fit cache lines - all while understanding the intricate details of their target hardware.
 Figure 3: The trade-off between expressiveness and optimization potential
Figure 3: The trade-off between expressiveness and optimization potential
This situation suggests a radical solution: what if we gave up Turing completeness? By adopting a more restricted programming model, we could enable compilers to precisely determine when and how a program will execute. This would allow us to explore all possible execution strategies during compilation and find the optimal one. While finding the absolute optimal solution is likely NP-complete - especially when considering hardware intricacies like micro-ops, hidden latencies, and kernel-specific overheads - these complexities are largely artifacts of our current approach to optimization.
With full control over the execution schedule, we could eliminate many of these complexities. We would know exactly when each instruction will execute, making it trivial to determine the fastest solution among alternatives. We could precisely orchestrate the overlap of computation and communication, identify bottlenecks, and optimize the entire system’s performance.
The NP-completeness of this problem might seem daunting, but there are several factors that make it tractable in practice:
-
Symmetrical Systems: Modern hardware is highly symmetrical. GPUs have uniform cores with identical L1 caches, evenly distributed L2 caches, and when using multiple nodes, they’re typically equivalent. This symmetry means solutions for one subsystem often apply to the entire system, allowing us to break the problem into smaller, manageable chunks.
-
Simple Operations: The programs we’re targeting - matrix multiplications, reductions, softmax operations - are relatively simple and have limited interactions. These operations are highly regular and don’t have complex sequential dependencies, making them much easier to optimize than arbitrary Turing-complete programs.
-
Modular Solutions: The symmetrical nature of our target systems means we can often find solutions for parts of the system and apply them to similar components, reducing the overall complexity of the optimization problem.
It’s important to note that this approach won’t solve all problems. Complex programs with intricate sequential dependencies and arbitrary Turing-complete computations will still be challenging to optimize for distributed systems. However, for the specific class of problems we’re targeting - large-scale numerical computations and machine learning workloads - this approach offers a promising path forward.
A New Approach
Let’s start with a simple example: summing the elements of a vector. In traditional Rust, we might write something like this:
fn sum_vector(v: &[f32]) -> f32 {
v.iter().sum()
}
This function is concise but leaves many important questions unanswered: Where does the vector live? How many elements does it have? Should we use a GPU for this computation? What if we have multiple nodes available?
Now, consider a version where we provide this information through type annotations:
fn sum_vector(v: &[f32; N] @ Disk) -> f32 @ RAM {
v.iter().sum()
}
This annotated version tells the compiler crucial information:
- The vector has N elements
- The input data lives on disk
- The result should be stored in RAM
With this information, the compiler can make intelligent decisions:
- For small N (e.g., 4 elements), it might choose a single CPU implementation
- For large N (e.g., 1 million elements), it might distribute the computation across GPUs or nodes
- If the input is on disk, it can plan the data movement accordingly
- It can generate multiple code paths optimized for different input sizes
The key insight is that N doesn’t need to be known at compile time. We could specify a range of possible values:
fn sum_vector(v: &[f32; N] @ Disk) -> f32 @ RAM
where
N: Range<4, 1_000_000>
{
v.iter().sum()
}
The compiler can then:
- Analyze the performance characteristics for different N values
- Determine the breakpoints where different strategies become optimal
- Generate multiple code paths
- Choose the appropriate path at runtime based on the actual input size
This approach allows us to:
- Make optimal decisions based on data characteristics
- Generate specialized code for different scenarios
- Handle data movement efficiently
- Adapt to the available hardware resources
The compiler becomes an active participant in optimization, using the type information to make informed decisions about:
- Data distribution
- Computation strategy
- Memory management
- Hardware utilization
Compiler-Driven Optimization
At first glance, one might worry that this approach would lead to verbose, annotation-laden code. After all, our example shows type annotations for data location, and it’s natural to be concerned about this complexity spreading throughout the codebase. However, this isn’t the case. Most functions in a program won’t need these annotations at all, because we don’t need to specify where intermediate computations happen.
The annotations only appear at the boundaries of our computation - the entry points where data first enters our system (like reading from disk or receiving network data) and the exit points where we need the results in a specific location (like writing to a file or sending data over the network). These are the only places where we truly care about data location, as they represent the interfaces between our program and the outside world.
 Figure 4: How the compiler manages data location decisions
Figure 4: How the compiler manages data location decisions
This approach allows the compiler to make intelligent decisions about data placement. For instance, in our vector sum example, if the data is already on the GPU from previous computations, the compiler can choose to keep it there rather than moving it to the CPU. The same function might execute on different hardware depending on the program’s current state.
The compiler handles the complexity of:
- Tracking where data lives throughout the program
- Making decisions about data placement
- Adapting to the current execution context
- Minimizing data movement
The Benefits
This approach offers several key advantages:
- Developers can focus on algorithms rather than implementation details
- The compiler can make global optimizations across the entire system
- The compiler can add Byzantine fault tolerance checks at system boundaries, detecting and adapting to nodes that are performing poorly or failing
- The compilation phase can predict exact execution times, enabling runtime verification of system behavior and detection of hardware issues